Resistencia electrica
Se le llama resistencia eléctrica a la mayor o menor oposición que tienen los electrones para desplazarse a través de un conductor. La unidad de resistencia en el sistema internacional es el ohm, que se representa con la letra griega omega (Ω), en honor al físico alemán George Ohm, quien descubrió el principio que ahora lleva su nombre. La resistencia está dada por la siguiente fórmula:
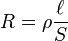
En donde ρ es el coeficiente de proporcionalidad o la resistividad del material.
La resistencia de un material depende directamente de dicho coeficiente, además es directamente proporcional a su longitud (aumenta conforme es mayor su longitud) y es inversamente proporcional a su sección transversal (disminuye conforme aumenta su grosor o sección transversal).
Origen
Descubierta por Georg Ohm en 1827, la resistencia eléctrica tiene un parecido conceptual a la fricción en la física mecánica. La unidad de la resistencia en el Sistema Internacional de Unidades es el ohmio (Ω). Para su medición en la práctica existen diversos métodos, entre los que se encuentra el uso de un ohmímetro. Además, su cantidad recíproca es la conductancia, medida en Siemens.
Además, de acuerdo con la ley de Ohm la resistencia de un material puede definirse como la razón entre la diferencia de potencial eléctrico y la corriente en que atraviesa dicha resistencia, así:

Donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente en amperios.
También puede decirse que "la intensidad de la corriente que pasa por un conductor es directamente proporcional a la longitud e inversamente proporcional a su resistencia"
Según sea la magnitud de esta medida, los materiales se pueden clasificar en conductores, aislantes y semiconductor. Existen además ciertos materiales en los que, en determinadas condiciones de temperatura, aparece un fenómeno denominado superconductividad, en el que el valor de la resistencia es prácticamente nulo.
Comportamientos ideales y reales
Una resistencia ideal es un elemento pasivo que disipa energía en forma de calor según la ley de Joule]]. También establece una relación de proporcionalidad entre la intensidad de corriente que la atraviesa y la tensión medible entre sus extremos, relación conocida como ley de Ohm:

Donde i (t) es la corriente eléctrica que atraviesa la resistencia de valor R y u (t) es la diferencia de potencial que se origina. En general, una resistencia real podrá tener diferente comportamiento en función del tipo de corriente que circule por ella.
Comportamiento en corriente continua
Una resistencia real en corriente continua (CC) se comporta prácticamente de la misma forma que si fuera ideal, esto es, transformando la energía eléctrica en calor por efecto Joule. La ley de Ohm para corriente continua establece que:
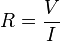
Donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente en amperios.
Comportamiento en corriente alterna
Una resistencia real muestra un comportamiento diferente del que se observaría en una resistencia ideal si la intensidad que la atraviesa no es continua. En el caso de que la señal aplicada sea senoidal, corriente alterna (CA), a bajas frecuencias se observa que una resistencia real se comportará de forma muy similar a como lo haría en CC, siendo despreciables las diferencias. En altas frecuencias el comportamiento es diferente, aumentando en la medida en la que aumenta la frecuencia aplicada, lo que se explica fundamentalmente por los efectos inductivos que producen los materiales que conforman la resistencia real.

Asociacion de resistencias
Resistencia equivalente
Se denomina resistencia equivalente de una asociación respecto de dos puntos A y B, a aquella que conectada a la misma diferencia de potencial, UAB, demanda la misma intensidad, Esto significa que ante las mismas condiciones, la asociación y su resistencia equivalente disipan la misma potencia.

Asociacion en serie
Dos o más resistencias se encuentran conectadas en serie cuando al aplicar al conjunto una diferencia de potencial, todas ellas son recorridas por la misma corriente.
Para determinar la resistencia equivalente de una asociación serie imaginaremos que ambas, están conectadas a la misma diferencia de potencial, UAB. Si aplicamos la segunda ley de Kirchhoff a la asociación en serie tendremos:
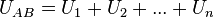
Aplicando la ley de Ohm:

En la resistencia equivalente:

Finalmente, igualando ambas ecuaciones se obtiene que:

Y eliminando la intensidad:
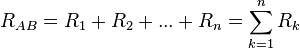
Por lo tanto, la resistencia equivalente a n resistencias montadas en serie es igual a la sumatoria de dichas resistencias.
Asociacion en paralelo
Dos o más resistencias se encuentran en paralelo cuando tienen dos terminales comunes de modo que al aplicar al conjunto una diferencia de potencial, UAB, todas las resistencias tienen la misma caída de tensión, UAB.
Para determinar la resistencia equivalente de una asociación en paralelo imaginaremos que ambas, están conectadas a la misma diferencia de potencial mencionada, UAB, lo que originará una misma demanda de corriente eléctrica, Esta corriente se repartirá en la asociación por cada una de sus resistencias de acuerdo con la primera ley de Kirchhoff:
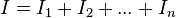
Asociacion mixta
En una asociación mixta podemos encontrarnos conjuntos de resistencias en serie con conjuntos de resistencias en paralelo.
A veces una asociación mixta es necesaria ponerla en modo texto. Para ello se utilizan los símbolos "+" y "//" para designar las asociaciones serie y paralelo respectivamente. Así con (R1 + R2) se indica que R1 y R2 están en serie mientras que con (R1//R2) que están en paralelo.
a) (R1//R2)+ (R3//R4)
b) (R1+R3)// (R2+R4)
c) ((R1+R2)//R3)+R4
Asociacion de estrella y triangulo
También llamadas y o delta respectivamente. Este tipo de asociaciones son comunes en las cargas trifásicas. Las ecuaciones de equivalencia entre ambas asociaciones vienen dadas por el teorema de Kennelly:
Resistencias en estrella en función de las resistencias en triángulo (transformación de triángulo a estrella)
El valor de cada una de las resistencias en estrella es igual al cociente del producto de las dos resistencias en triángulo adyacentes al mismo terminal entre la suma de las tres resistencias en triángulo.
El valor de cada una de las resistencias en estrella es igual al cociente del producto de las dos resistencias en triángulo adyacentes al mismo terminal entre la suma de las tres resistencias en triángulo.
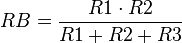
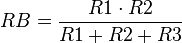

Asociacion puente
Si en una asociación paralela de serie se conecta una resistencia que una las dos ramas en paralelo, se obtiene una asociación puente.
La determinación de la resistencia equivalente de este tipo de asociación tiene sólo interés pedagógico. Para ello se sustituye bien una de las configuraciones en triángulo de la asociación, la R1-R2-R5 o la R3-R4-R5 por su equivalente en estrella, bien una de las configuraciones en estrella, la R1-R3-R5 o la R2-R4-R5 por su equivalente en triángulo. En ambos casos se consigue transformar el conjunto en una asociación mixta de cálculo sencillo. Otro método consiste en aplicar una fem (E) a la asociación y obtener su resistencia equivalente como relación de dicha fem y la corriente total demandada (E/I).
El interés de este tipo de asociación está en el caso en el que por la resistencia central, R5, no circula corriente o R4, en función de las otras tres. En ello se basan los puentes de Wheatstone y de hilo para la Medida de resistencias con precisión.
Resistencia de un conductor
El conductor es el encargado de unir eléctricamente cada uno de los componentes de un circuito. Dado que tiene resistencia óhmica, puede ser considerado como otro componente más con características similares a las de la resistencia eléctrica.
De este modo, la resistencia de un conductor eléctrico es la medida de la oposición que presenta al movimiento de los electrones en su seno, es decir la oposición que presenta al paso de la corriente eléctrica. Generalmente su valor es muy pequeño y por ello se suele despreciar, esto es, se considera que su resistencia es nula (conductor ideal), pero habrá casos particulares en los que se deberá tener en cuenta su resistencia (conductor real).
La resistencia de un conductor depende de la longitud del mismo () en m, de su sección () en m², del tipo de material y de la temperatura. Si consideramos la temperatura constante (20 ºC), la resistencia viene dada por la siguiente expresión:
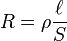
En la que es la resistividad (una característica propia de cada material).
Codigo de colores

Tipos de resistencia
Resistencia de hilo bobindado
Fueron de los primeros tipos en fabricarse, y aún se utilizan cuando se requieren potencias algo elevadas de disipación. Están constituidas por un hilo conductor bobinado en forma de hélice o espiral (a modo de rosca de tornillo) sobre un sustrato cerámico.

Resistencia de carbon prensado
Estas fueron también de las primeras en fabricarse en los albores de la electrónica. Están constituidas en su mayor parte por grafito en polvo, el cual se prensa hasta formar un tubo.

Resistencias de pelicula de carbon
Este tipo es muy habitual hoy día, y es utilizado para valores de hasta 2 vatios. Se utiliza un tubo cerámico como sustrato sobre el que se deposita una película de carbón.

Resistencias de pelicula de oxido metalico
Son muy similares a las de película de carbón en cuanto a su modo de fabricación, pero son más parecidas, eléctricamente hablando a las de película metálica. Se hacen igual que las de película de carbón, pero sustituyendo el carbón por una fina capa de óxido metálico (estaño o latón). Estas resistencias son más caras que las de película metálica, y no son muy habituales. Se utilizan en aplicaciones militares (muy exigentes) o donde se requiera gran fiabilidad, porque la capa de óxido es muy resistente a daños mecánicos y a la corrosión en ambientes húmedos.

Resistencias de pelicula metalica
Este tipo de resistencia es el que mayoritariamente se fabrica hoy día, con unas características de ruido y estabilidad mejoradas con respecto a todas las anteriores. Tienen un coeficiente de temperatura muy pequeño, del orden de 50 ppm/°C (partes por millón y grado Centígrado). También soportan mejor el paso del tiempo, permaneciendo su valor en ohmios durante un mayor período de tiempo. Se fabrican este tipo de resistencias de hasta 2 watios de potencia, y con tolerancias del 1% como tipo estándar.

Resistencias de metal vidreado
Son similares a las de película metálica, pero sustituyendo la película metálica por otra compuesta por vidrio con polvo metálico. Como principal característica cabe destacar su mejor comportamiento ante sobrecargas de corriente, que puede soportar mejor por su inercia térmica que le confiere el vidrio que contiene su composición. Como contrapartida, tiene un coeficiente térmico peor, del orden de 150 a 250 ppm/°C. Se dispone de potencias de hasta 3 vatios.
Se dispone de estas resistencias encapsuladas en chips tipo DIL (dual in line) o SIL (single in line).

Resistencias dependientes de la temperatura
Aunque todas las resistencias, en mayor o menor grado, dependen de la temperatura, existen unos dispositivos específicos que se fabrican expresamente para ello, de modo que su valor en ohmios dependa "fuertemente" de la temperatura. Se les denomina termistores y como cabía esperar, poseen unos coeficientes de temperatura muy elevados, ya sean positivos o negativos. Coeficientes negativos implican que la resistencia del elemento disminuye según sube la temperatura, y coeficientes positivos al contrario, aumentan su resistencia con el aumento de la temperatura. El silicio, un material semiconductor, posee un coeficiente de temperatura negativo. A mayor temperatura, menor resistencia. Esto ocasiona problemas, como el conocido efecto de "avalancha térmica" que sufren algunos dispositivos semiconductores cuando se eleva su temperatura lo suficiente, y que puede destruir el componente al aumentar su corriente hasta sobrepasar la corriente máxima que puede soportar.
A los dispositivos con coeficiente de temperatura negativo se les denomina NTC (negative temperature coefficient).
A los dispositivos con coeficiente de temperatura positivo se les denomina PTC (positive temperature coefficient).
Una aplicación típica de un NTC es la protección de los filamentos de válvula, que son muy sensibles al "golpe" de encendido o turn-on. Conectando un NTC en serie protege del golpe de encendido, puesto que cuando el NTC está a temperatura ambiente (frío, mayor resistencia) limita la corriente máxima y va aumentando la misma según aumenta la temperatura del NTC, que a su vez disminuye su resistencia hasta la resistencia de régimen a la que haya sido diseñado. Hay que elegir correctamente la corriente del dispositivo y la resistencia de régimen, así como la tensión que caerá en sus bornas para que el diseño funcione correctamente.

